Funded by Department of Energy, grant DE-SC0019303 AFOSR, grants FA9550-18-1-0023 and FA9550-21-1-0084 AFOSR and AFRL, grant FA9550-17-1-0195
In collaboration with former group members Mengwu Guo (University of Twente), Boris Kramer (UCSD), Benjamin Peherstorfer (NYU), Elizabeth Qian (Caltech)
Researchers:
Ionut Farcas, Oden Institute postdoc
Rudy Geelen, Oden Institute Postdoc
Parisa Khodabakhshi, Oden Institute Postdoc
Shane McQuarrie, Oden Institute PhD student
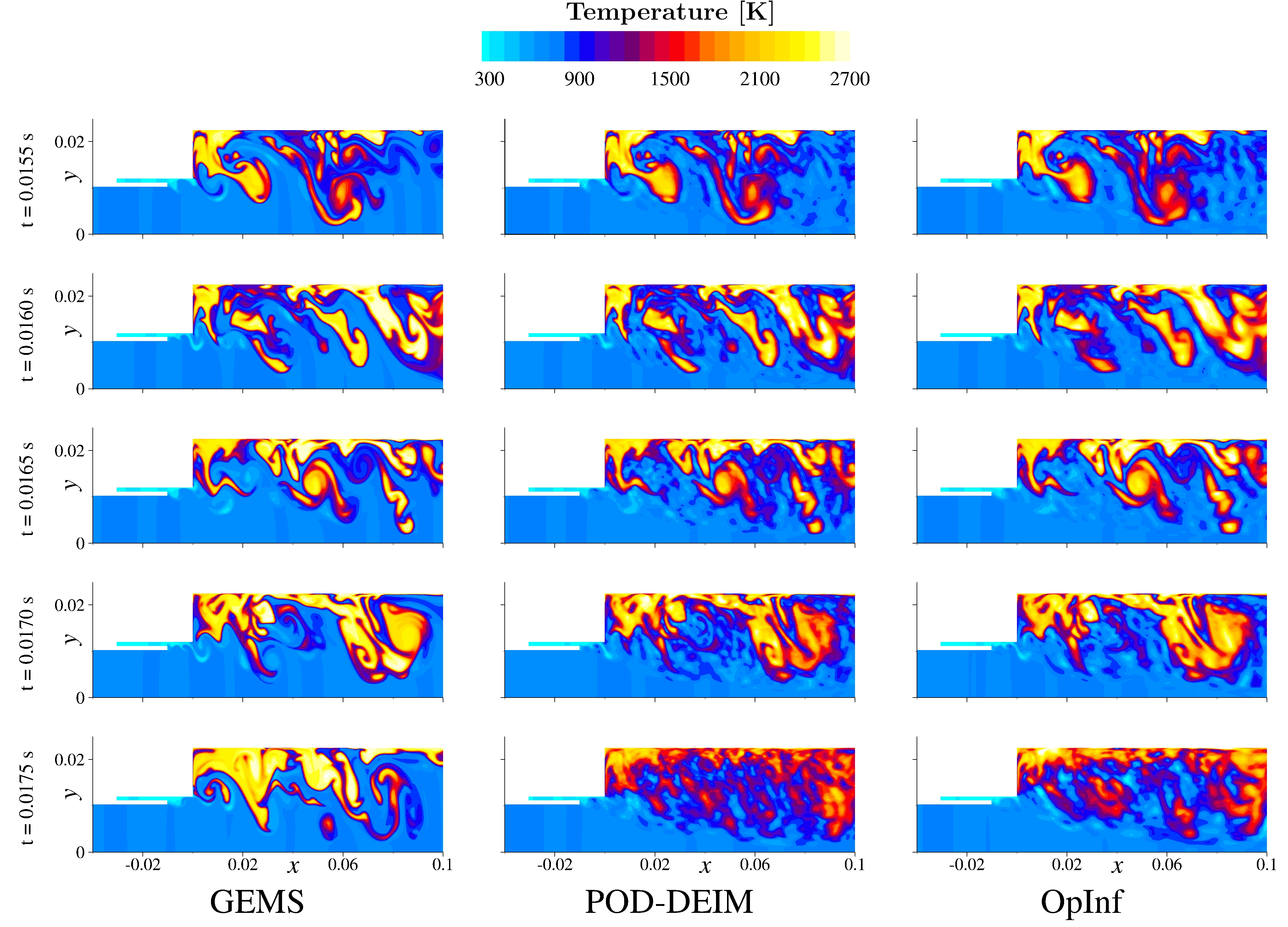
Operator Inference learns reduced models non-intrusively from simulation data. This makes the approach easy to apply to commerical and legacy codes, such as this example of the General Mesh and Equation Solver (GEMS).
Open source codes
Access a Python implementation of Operator Inference here on Github.
Relevant publications
McQuarrie, S., Huang, C. and Willcox, K., Data-driven reduced-order models via regularized operator inference for a single-injector combustion process. To appear Journal of the Royal Society of New Zealand, 2021, DOI: 10.1080/03036758.2020.1863237. [abstract]
Qian, E., Farcas, I., and Willcox, K., Reduced operator inference for nonlinear partial differential equations. arXiv preprint arXiv:2102.00083, 2021.
Khodabakhshi, P. and Willcox, K. Non-intrusive data-driven model reduction for differential algebraic equations derived from lifting transformations. Oden Institute Report 21-08, Oden Institute for Computational Engineering and Sciences, The University of Texas at Austin, April 2021.
Qian, E., Kramer, B., Peherstorfer, B., and Willcox, K., Lift & Learn: Physics-informed machine learning for large-scale nonlinear dynamical systems. Physica D: Nonlinear Phenomena, Volume 406, May 2020, 132401. [abstract]
Swischuk, R., Kramer, B., Huang, C., and Willcox, K., Learning physics-based reduced-order models for a single-injector combustion process. AIAA Journal, Vol. 58, No. 6, June 2020, pp. 2658-2672. [abstract]
Benner, P., Goyal, P., Kramer, B., Peherstorfer, B., and Willcox, K., Operator inference for non-intrusive model reduction of systems with non-polynomial nonlinear terms. Computer Methods in Applied Mechanics and Engineering, Vol. 372, pp. 113433, December 2020. [abstract]
Qian, E., Kramer, B., Marques, A., Willcox, K., Transform & Learn: A data-driven approach to nonlinear model reduction.. AIAA Aviation 2019 Forum, June 2019, Dallas, TX. DOI 10.2514/6.2019-3707. [abstract]
Peherstorfer, B. and Willcox, K., Data-driven operator inference for nonintrusive projection-based model reduction, Computer Methods in Applied Mechanics and Engineering, Vol. 306, pp. 196-215, 2016. [abstract]
Operator Inference is a scientific machine learning approach that blends data-driven learning with physics-based modeling.
We start with a physics-based model (usually a system of partial differential equations). Next, we exploit the fact that a projection-based reduced model evolves in a low-dimensional coordinate space but has the same structured form of the model defined by the physics. Putting these two together defines the form of the low-dimensional model we seek. This model is parameterized by low-dimensional operators. Operator Inference determines this structured model by solving a regression problem to find the reduced-order operators. The regression problem is linear in the unknown operators and can thus be solved efficiently and at scale.
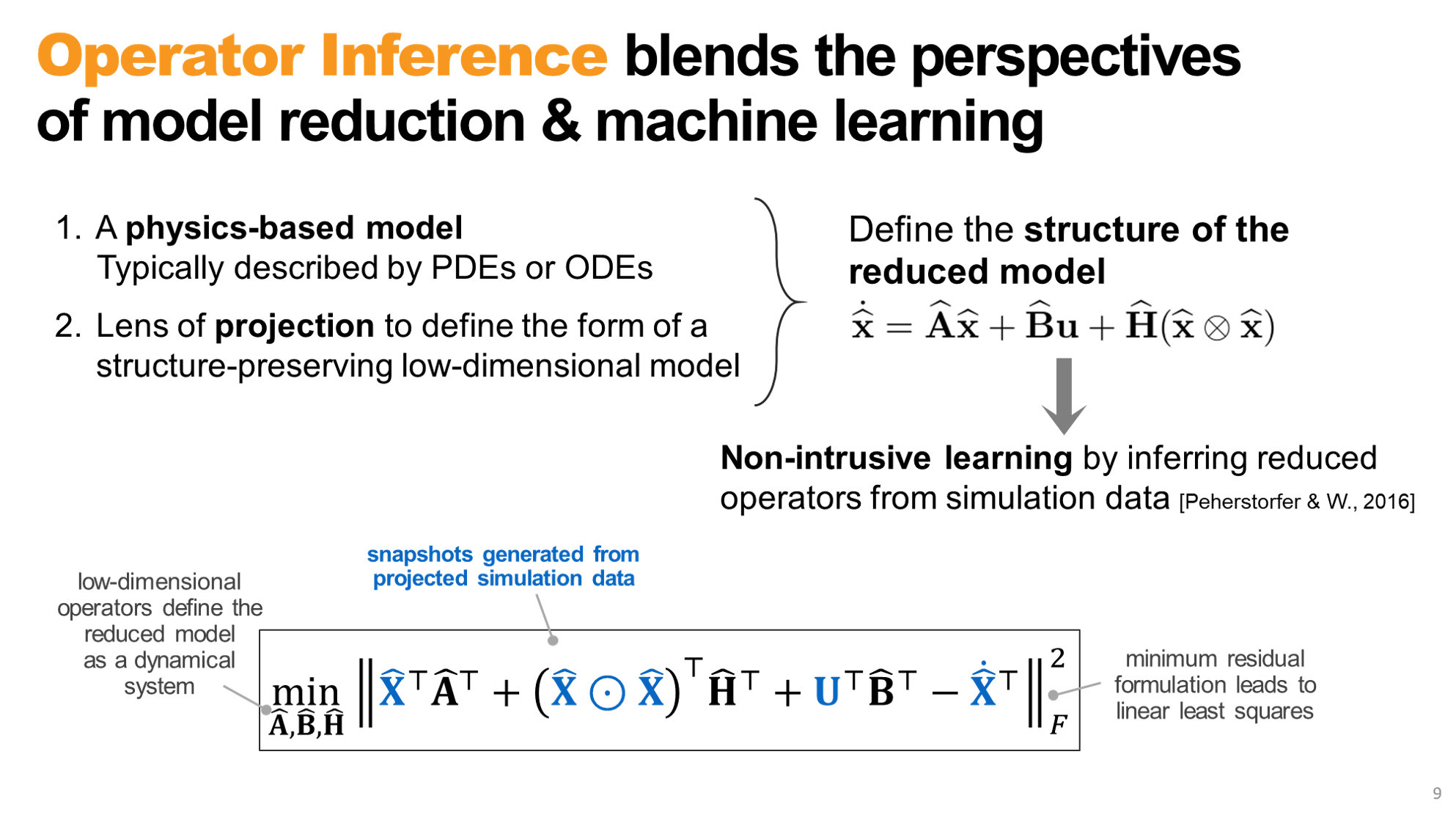
Operator Inference blends the perspectives of machine learning and reduced-order modeling to embed physics constraints in the learning process.
Operator Inference has a number of advantages over other model reduction and scientific machine learning approaches:
We are applying Operator Inference in a number of different application settings, including rocket combustion, additive manufacturing and fluid mechanics.
McQuarrie, S., Huang, C. and Willcox, K. Journal of the Royal Society of New Zealand, 2021, DOI:10.1080/03036758.2020.1863237
This paper derives predictive reduced-order models for rocket engine combustion dynamics via Operator Inference, a scientific machine learning approach that blends data-driven learning with physics-based modeling. The non-intrusive nature of the approach enables variable transformations that expose system structure. The specific contribution of this paper is to advance the formulation robustness and algorithmic scalability of the Operator Inference approach. Regularization is introduced to the formulation to avoid over-fitting. The task of determining an optimal regularization is posed as an optimization problem that balances training error and stability of long-time integration dynamics. A scalable algorithm and open-source implementation are presented, then demonstrated for a single-injector rocket combustion example. This example exhibits rich dynamics that are difficult to capture with state-of-the-art reduced models. With appropriate regularization and an informed selection of learning variables, the reduced-order models exhibit high accuracy in re-predicting the training regime and acceptable accuracy in predicting future dynamics, while achieving close to a million times speedup in computational cost. When compared to a state-of-the-art model reduction method, the Operator Inference models provide the same or better accuracy at approximately one thousandth of the computational cost.
Qian, E., Kramer, B., Peherstorfer, B., and Willcox, K., Physica D: Nonlinear Phenomena, Volume 406, May 2020, 132401.
We present Lift & Learn, a physics-informed method for learning low-dimensional models for large-scale dynamical systems. The method exploits knowledge of a system's governing equations to identify a coordinate transformation in which the system dynamics have quadratic structure. This transformation is called a lifting map because it often adds auxiliary variables to the system state. The lifting map is applied to data obtained by evaluating a model for the original nonlinear system. This lifted data is projected onto its leading principal components, and low-dimensional linear and quadratic matrix operators are fit to the lifted reduced data using a least-squares operator inference procedure. Analysis of our method shows that the Lift & Learn models are able to capture the system physics in the lifted coordinates at least as accurately as traditional intrusive model reduction approaches. This preservation of system physics makes the Lift & Learn models robust to changes in inputs. Numerical experiments on the FitzHugh-Nagumo neuron activation model and the compressible Euler equations demonstrate the generalizability of our model.
Swischuk, R., Kramer, B., Huang, C. and Willcox, K. AIAA Journal, Vol. 58, No. 6, June 2020, pp. 2658-2672. Also in Proceedings of 2020 AIAA SciTech Forum & Exhibition, Orlando FL, January, 2020. Also Oden Institute Report 19-13.
This paper presents a physics-based data-driven method to learn predictive reduced-order models (ROMs) from high-fidelity simulations, and illustrates it in the challenging context of a single-injector combustion process. The method combines the perspectives of model reduction and machine learning. Model reduction brings in the physics of the problem, constraining the ROM predictions to lie on a subspace defined by the governing equations. This is achieved by defining the ROM in proper orthogonal decomposition (POD) coordinates, which embed the rich physics information contained in solution snapshots of a high-fidelity computational fluid dynamics (CFD) model. The machine learning perspective brings the flexibility to use transformed physical variables to define the POD basis. This is in contrast to traditional model reduction approaches that are constrained to use the physical variables of the high-fidelity code. Combining the two perspectives, the approach identifies a set of transformed physical variables that expose quadratic structure in the combustion governing equations and learns a quadratic ROM from transformed snapshot data. This learning does not require access to the high-fidelity model implementation. Numerical experiments show that the ROM accurately predicts temperature, pressure, velocity, species concentrations, and the limit-cycle amplitude, with speedups of more than five orders of magnitude over high-fidelity models. Our ROM simulation is shown to be predictive 200% past the training interval. ROM-predicted pressure traces accurately match the phase of the pressure signal and yield good approximations of the limit-cycle amplitude.
Benner, P., Goyal, P., Kramer, B., Peherstorfer, B., and Willcox, K. Computer Methods in Applied Mechanics and Engineering, Vol. 372, pp. 113433, December 2020.
This work presents a non-intrusive model reduction method to learn low-dimensional models of dynamical systems with non-polynomial nonlinear terms that are spatially local and that are given in analytic form. In contrast to state-of-the-art model reduction methods that are intrusive and thus require full knowledge of the governing equations and the operators of a full model of the discretized dynamical system, the proposed approach requires only the non-polynomial terms in analytic form and learns the rest of the dynamics from snapshots computed with a potentially black-box full-model solver. The proposed method learns operators for the linear and polynomially nonlinear dynamics via a least-squares problem, where the given non-polynomial terms are incorporated in the right-hand side. The least-squares problem is linear and thus can be solved efficiently in practice. The proposed method is demonstrated on three problems governed by partial differential equations, namely the diffusion-reaction Chafee-Infante model, a tubular reactor model for reactive flows, and a batch-chromatography model that describes a chemical separation process. The numerical results provide evidence that the proposed approach learns reduced models that achieve comparable accuracy as models constructed with state-of-the-art intrusive model reduction methods that require full knowledge of the governing equations.
Qian, E., Kramer, B., Marques, A., Willcox, K., AIAA Aviation 2019 Forum, June 2019, Dallas, TX. DOI 10.2514/6.2019-3707.
This paper presents Transform & Learn, a physics-informed surrogate modeling approach that unites the perspectives of model reduction and machine learning. The proposed method uses insight from the physics of the problem - in the form of partial differential equation (PDE) models - to derive a state transformation in which the system admits a quadratic representation. Snapshot data from a high-fidelity model simulation are transformed to the new state representation and subsequently are projected onto a low-dimensional basis. The quadratic reduced model is then learned via a least-squares-based operator inference procedure. The state transformation thus plays two key roles in the proposed method: it allows the task of nonlinear model reduction to be reformulated as a structured model learning problem, and it parametrizes the machine learning problem in a way that recovers efficient, generalizable models. The proposed method is demonstrated on two PDE examples. First, we transform the Euler equations in conservative variables to the specific volume state representation, yielding low-dimensional Transform & Learn models that achieve a 0.05% relative state error when compared to a high-fidelity simulation in the conservative variables. Second, we consider a model of the Continuously Variable Resonance Combustor, a single element liquid-fueled rocket engine experiment. We show that the specific volume representation of this model also has quadratic structure and that the learned quadratic reduced models can accurately predict the growing oscillations of an unstable combustor.
Peherstorfer, B. and Willcox, K., Computer Methods in Applied Mechanics and Engineering, Vol. 306, pp. 196-215, 2016.
This work presents a nonintrusive projection-based model reduction approach for full models based on time-dependent partial differential equations. Projection-based model reduction constructs the operators of a reduced model by projecting the equations of the full model onto a reduced space. Traditionally, this projection is intrusive, which means that the full-model operators are required either explicitly in an assembled form or implicitly through a routine that returns the action of the operators on a given vector; however, in many situations the full model is given as a black box that computes trajectories of the full-model states and outputs for given initial conditions and inputs, but does not provide the full-model operators. Our non-intrusive operator inference approach infers approximations of the reduced operators from the initial conditions, inputs, trajectories of the states, and outputs of the full model, without requiring the full-model operators. Our operator inference is applicable to full models that are linear in the state or have a low-order polynomial nonlinear term. The inferred operators are the solution of a least-squares problem and converge, with sufficient state trajectory data, in the Frobenius norm to the reduced operators that would be obtained via an intrusive projection of the full-model operators. Our numerical results demonstrate operator inference on a linear climate model and on a tubular reactor model with a polynomial nonlinear term of third order.