This example demonstrates our data-driven reduced models based on online adaptive DEIM. The reduced models learn from sparse samples (magenta squares) of the target function low-rank updates to the DEIM basis (blue, right). In doing so, the data-driven reduced models capture the nonlinear behavior of the target function more accurately (right) than classical, static DEIM (left).

Relevant publications
Peherstorfer, B. and Willcox, K., Online Adaptive Model Reduction for Nonlinear Systems via Low-Rank Updates, SIAM Journal on Scientific Computing , Vol. 37, No. 4, pp. A2123-A2150, 2015.
Mainini, L. and Willcox, K. A surrogate modeling approach to support real-time structural assessment and decision-making, AIAA Journal, Vol. 53, No. 6, pp. 1612-1626, 2015.
Cui, T., Marzouk, Y. and Willcox, K. Data-driven model reduction for the Bayesian solution of inverse problems, International Journal for Numerical Methods in Engineering, Vol. 102, No. 5, pp. 966-990, published online 15 August, 2014, DOI: 10.1002/nme.4748.
Peherstorfer, B. and Willcox, K., Dynamic data-driven reduced-order models, Computer Methods in Applied Mechanics and Engineering , Vol. 291, pp. 21-41, 2015.
Peherstorfer, B. and Willcox, K., Dynamic data-driven model reduction: Adapting reduced models from incomplete data, Advanced Modeling and Simulation in Engineering Sciences , 3(11), Springer, 2016.
In data-driven model reduction, the reduced model is adapted using data collected as the computation proceeds.
Classical model reduction follows a decomposition of computational tasks into two phases: (1) the offline phase where the reduced model is derived from the full model with one-time high costs, and (2) the online phase where the reduced model is used (but typically stays fixed). In data-driven model reduction, we derive an initial reduced model in the offline phase, but then we use data from the online phase to adapt the reduced model.
Why do we need data-driven model reduction? It is often the case that only limited data and information for building the reduced model are available in the offline phase. For example, in outer-loop applications (such as optimization, inverse problems, and control), the solution path is unknown in the offline phase. This can lead to situations where the reduced model is used to approximate a full-model solution that is very different to the scenarios considered in the offline phase, making the reduced model inaccurate. Our work on adaptive data-driven model reduction techniques compensates for this by learning from data generated during the online phase and using this data to adapt the reduced model.
Our research has demonstrated that our adaptive model reduction techniques lead to robust data-driven reduced models that provide valid approximations of the full model even outside of the parameter domains for which they were initially built offline. Additionally, we observe that our adaptive reduced models efficiently capture nonlinear structures in the solution manifold of the full model and therefore often provide more accurate approximations of full models with highly nonlinear behavior than static reduced models.
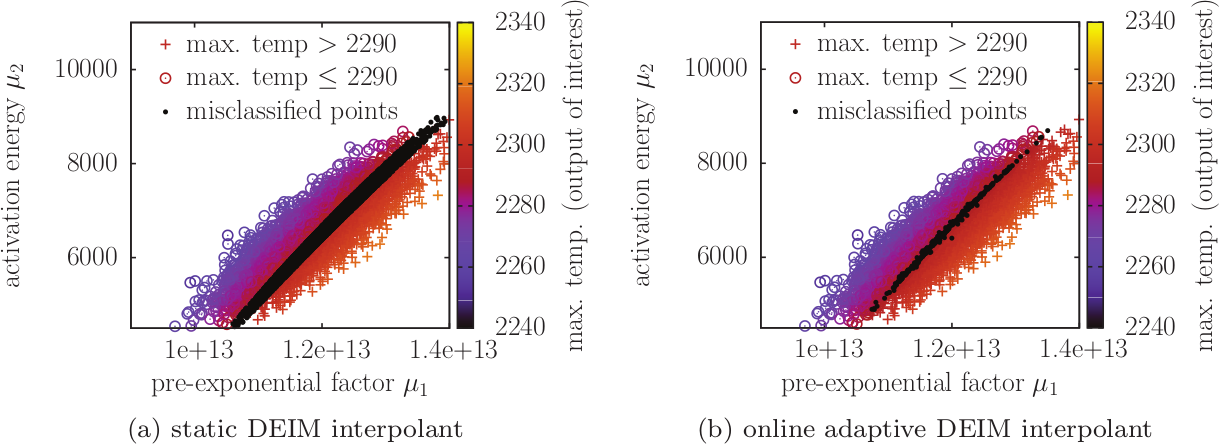
Our adaptive data-driven reduced models are updated while the computations proceed. Here: our adaptive discrete empirical interpolation method (DEIM) reduces the number of misclassified points by two orders of magnitude in an uncertainty quantification example.
Our data-driven model reduction techniques apply to general linear and nonlinear problems. In the linear setting, our (dynamic) data-driven reduced models rely on incremental reduced basis generation and incremental operator updates to adapt the reduced model to new snapshot data. For the nonlinear setting, we developed an online adaptive discrete empirical interpolation method (DEIM), which uses sparse data of the nonlinear term of the full model to derive optimal low-rank updates to the reduced model. Our work also contributes data-driven model reduction techniques that target specific applications such as inverse problems and structural assessment.
Peherstorfer, B. & Willcox, K. SIAM Journal on Scientific Computing, 37(4):A2123-A2150, SIAM, 2015
This work presents a nonlinear model reduction approach for systems of equations stemming from the discretization of partial differential equations with nonlinear terms. Our approach constructs a reduced system with proper orthogonal decomposition and the discrete empirical interpolation method (DEIM); however, whereas classical DEIM derives a linear approximation of the nonlinear terms in a static DEIM space generated in an offline phase, our method adapts the DEIM space as the online calculation proceeds and thus provides a nonlinear approximation. The online adaptation uses new data to produce a reduced system that accurately approximates behavior not anticipated in the offline phase. These online data are obtained by querying the full-order system during the online phase, but only at a few selected components to guarantee a computationally efficient adaptation. Compared to the classical static approach, our online adaptive and nonlinear model reduction approach achieves accuracy improvements of up to three orders of magnitude in our numerical experiments with time-dependent and steady-state nonlinear problems. The examples also demonstrate that through adaptivity, our reduced systems provide valid approximations of the full-order systems outside of the parameter domains for which they were initially built in the offline phase.
Mainini, L. and Willcox, K. AIAA Journal, Vol. 53, No. 6, pp. 1612-1626, 2015.
This paper proposes a data-driven strategy to assist online rapid decision-making for an unmanned aerial vehicle that uses sensed data to estimate its structural state, uses this estimate to update its corresponding flight capabilities, and then dynamically re-plans its mission accordingly. Our approach comprises offline and online computational phases constructed to address the sense-plan-act information flow while avoiding a costly online inference step. During the offline phase, high-fidelity finite element simulations are used to construct reduced-order models and classification criteria: proper orthogonal decomposition approximations and self-organizing maps are combined to realize a fast mapping from measured quantities to system capabilities. During the online phase, the surrogate mapping is employed to directly estimate the vehicle's evolving structural capability from sensor data. The approach is demonstrated for a test problem of a composite wing panel on an unmanned aerial vehicle that undergoes degradation in structural properties.
Cui, T., Marzouk, Y. and Willcox, K. International Journal for Numerical Methods in Engineering, Vol. 102, No. 5, pp. 966-990, published online 15 August, 2014, DOI: 10.1002/nme.4748.
One of the major challenges in the Bayesian solution of inverse problems governed by partial differential equations (PDEs) is the computational cost of repeatedly evaluating numerical PDE models, as required by Markov chain Monte Carlo (MCMC) methods for posterior sampling. This paper proposes a data-driven projection-based model reduction technique to reduce this computational cost. The proposed technique has two distinctive features. First, the model reduction strategy is tailored to inverse problems: the snapshots used to construct the reduced-order model are computed adaptively from the posterior distribution. Posterior exploration and model reduction are thus pursued simultaneously. Second, to avoid repeated evaluations of the full-scale numerical model as in a standard MCMC method, we couple the full-scale model and the reduced-order model together in the MCMC algorithm. This maintains accurate inference while reducing its overall computational cost. In numerical experiments considering steady-state flow in a porous medium, the data-driven reduced-order model achieves better accuracy than a reduced-order model constructed using the classical approach. It also improves posterior sampling efficiency by several orders of magnitude compared with a standard MCMC method.
Peherstorfer, B. & Willcox, K. Computer Methods in Applied Mechanics and Engineering, 291:21-41, Elsevier, 2015.
Data-driven model reduction constructs reduced-order models of large-scale systems by learning the system response characteristics from data. Existing methods build the reduced-order models in a computationally expensive offline phase and then use them in an online phase to provide fast predictions of the system. In cases where the underlying system properties are not static but undergo dynamic changes, repeating the offline phase after each system change to rebuild the reduced-order model from scratch forfeits the savings gained in the online phase. This paper proposes dynamic reduced-order models that break with this classical but rigid approach. Dynamic reduced-order models exploit the opportunity presented by dynamic sensor data and adaptively incorporate sensor data during the online phase. This permits online adaptation to system changes while circumventing the expensive rebuilding of the model. A computationally cheap adaptation is achieved by constructing low-rank updates to the reduced operators. With these updates and with sufficient and accurate data, our approach recovers the same model that would be obtained by rebuilding from scratch. We demonstrate dynamic reduced-order models on a structural assessment example in the context of realtime decision making. We consider a plate in bending where the dynamic reduced-order model quickly adapts to changes in structural properties and achieves speedups of four orders of magnitude compared to rebuilding a model from scratch.
Peherstorfer, B. & Willcox, K. Advanced Modeling and Simulation in Engineering Sciences, 3(11), Springer, 2016
This work presents a data-driven online adaptive model reduction approach for systems that undergo dynamic changes. Classical model reduction constructs a reduced model of a large-scale system in an offline phase and then keeps the reduced model unchanged during the evaluations in an online phase; however, if the system changes online, the reduced model may fail to predict the behavior of the changed system. Rebuilding the reduced model from scratch is often too expensive in time-critical and real-time environments. We introduce a dynamic data-driven adaptation approach that adapts the reduced model from incomplete sensor data obtained from the system during the online computations. The updates to the reduced models are derived directly from the incomplete data, without recourse to the full model. Our adaptivity approach approximates the missing values in the incomplete sensor data with gappy proper orthogonal decomposition. These approximate data are then used to derive low-rank updates to the reduced basis and the reduced operators. In our numerical examples, incomplete data with 30-40% known values are sufficient to recover the reduced model that would be obtained via rebuilding from scratch.