Open source codes
Access a Python implementation of Operator Inference here on Github.
Relevant publications
Qian, E., Kramer, B., Peherstorfer, B., and Willcox, K., Lift & Learn: Physics-informed machine learning for large-scale nonlinear dynamical systems. Physica D: Nonlinear Phenomena, Volume 406, May 2020, 132401. [abstract]
Swischuk, R., Kramer, B., Huang, C., and Willcox, K., Learning physics-based reduced-order models for a single-injector combustion process. AIAA Journal, to appear, 2020. Also in Proceedings of 2020 AIAA SciTech Forum & Exhibition, Orlando FL, January, 2020. Also Oden Institute Report 19-13. [abstract]
Kramer, B., and Willcox, K., Balanced Truncation Model Reduction for Lifted Nonlinear Systems. arXiv:1907.12084. Submitted. [abstract]
Kramer, B. and Willcox, K., Nonlinear model order reduction via lifting transformations and proper orthogonal decomposition. AIAA Journal, Vol. 57 No. 6, pp. 2297-2307, 2019. [abstract]
Qian, E., Kramer, B., Marques, A. and Willcox, K., Transform & Learn: A data-driven approach to nonlinear model reduction. In Proceedings of AIAA Aviation Forum & Exhibition, Dallas, TX, June 2019. DOI 10.2514/6.2019-3707. [abstract]
Peherstorfer, B. and Willcox, K., Data-driven operator inference for nonintrusive projection-based model reduction, Computer Methods in Applied Mechanics and Engineering, Vol. 306, pp. 196-215, 2016. [abstract]
What is nonlinear model reduction?
Nonlinear model reduction uses projection to derive low-cost approximate models of nonlinear systems.
Why is nonlinear model reduction important?
Nonlinear systems model many different kinds of important physical phenomena in high-consequence applications across science, engineering and medicine. These nonlinear models are expensive to solve, making them intractable for design, parameter exploration, control, or real-time decision-making. This is where cheap reduced models are enablers.
Why is nonlinear model reduction difficult?
For linear systems, a projection-based reduced model has a compact easy-to-compute representation:
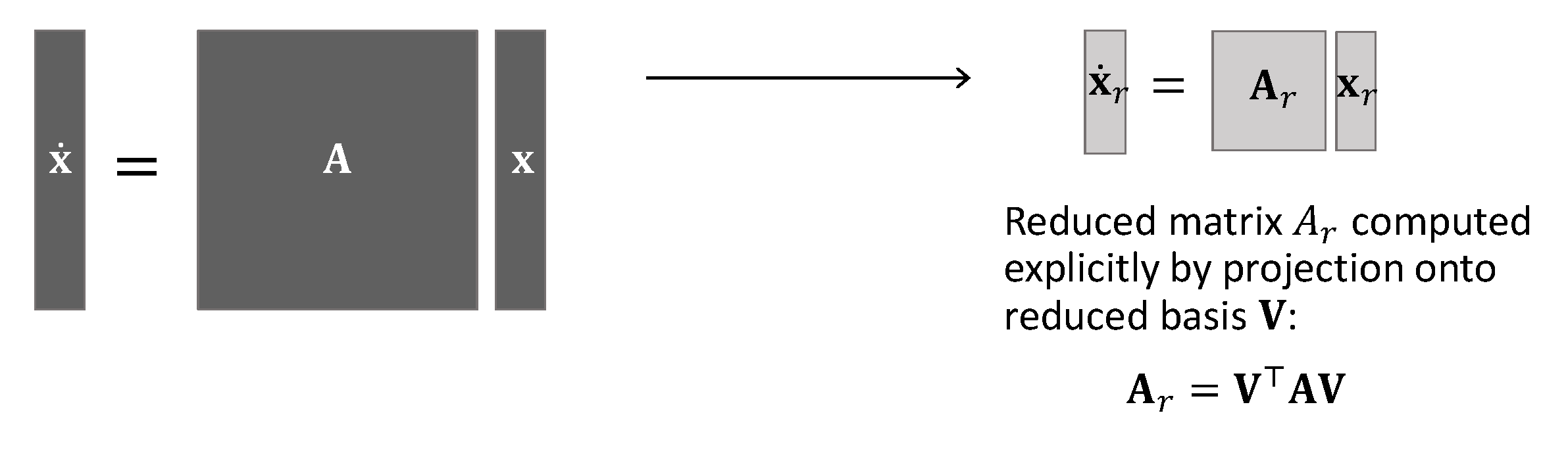 For a nonlinear system, the reduced operators cannot be explicitly computed without going back to the original expensive model:
For a nonlinear system, the reduced operators cannot be explicitly computed without going back to the original expensive model:
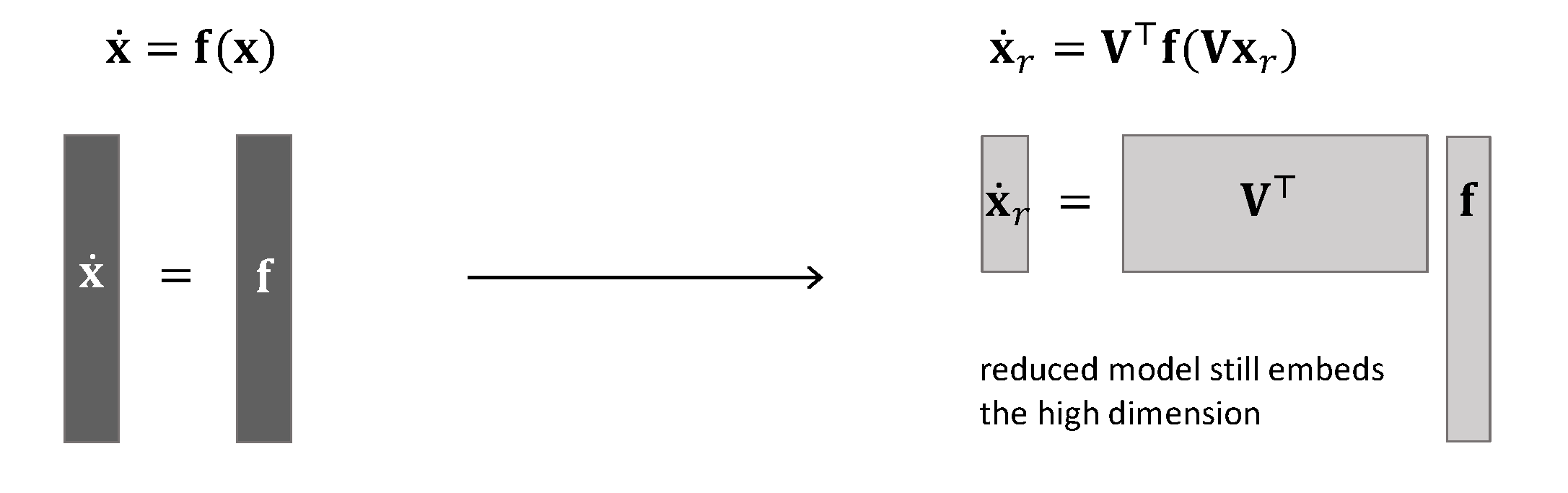
What are some state-of-the-art methods in nonlinear model reduction?
While the field of model reduction is mature for linear systems, reducing nonlinear systems remains a big challenge and an active area of research. The most popular method to reduce nonlinear systems is proper orthogonal decomposition (POD).
To make the resulting reduced models computationally efficient, POD is typically used together with a sparse sampling method (sometimes called "hyper-reduction") such as the missing point estimation (MPE), the empirical interpolation method (EIM), the discrete empirical interpolation method (DEIM), the Gappy POD method, or the Gauss-Newton with approximated tensors (GNAT) method. Our SIAM Review paper A Survey of Projection-Based Model Reduction Methods for Parametric Dynamical Systems has many references for these approaches.
Other methods for nonlinear model reduction use data-driven approaches via dynamic mode decomposition (DMD) and Operator Inference. More recently, certain input-independent model reduction methods such as balanced truncation and the iterative rational Krylov algorithm (IRKA) have been extended to quadratic-bilinear systems.
Our recent work has developed a new approach for nonlinear model reduction, enabled by data-driven learning of the reduced model through the structure-preserving lens of projection.
Our Lift & Learn approach has two key ingredients:
Access a Python implementation of Operator Inference here on Github.
LEARN: Learning a structured reduced model from data via Operator Inference
Given state snapshots and their time derivatives (called "velocity data" in the machine learning community), we solve a least squares problem to learn the operators of the reduced model. Under certain idealized conditions, we can recover the intrusive projection-based reduced model. The motivation of the original Operator Inference paper was non-intrusive model reduction (i.e., deriving reduced models for black-box problems where we do not have access to the high-fidelity operators to perform the projections). However, a powerful advantage of the data-driven Operator Inference approach is that it lets us learn a reduced model in any coordinates — we are not constrained to use the same physical variables as our high-fidelity model. This is where our second ingredient of variable transformations comes into play.
LIFT: Variable transformations that expose structure in the governing equations
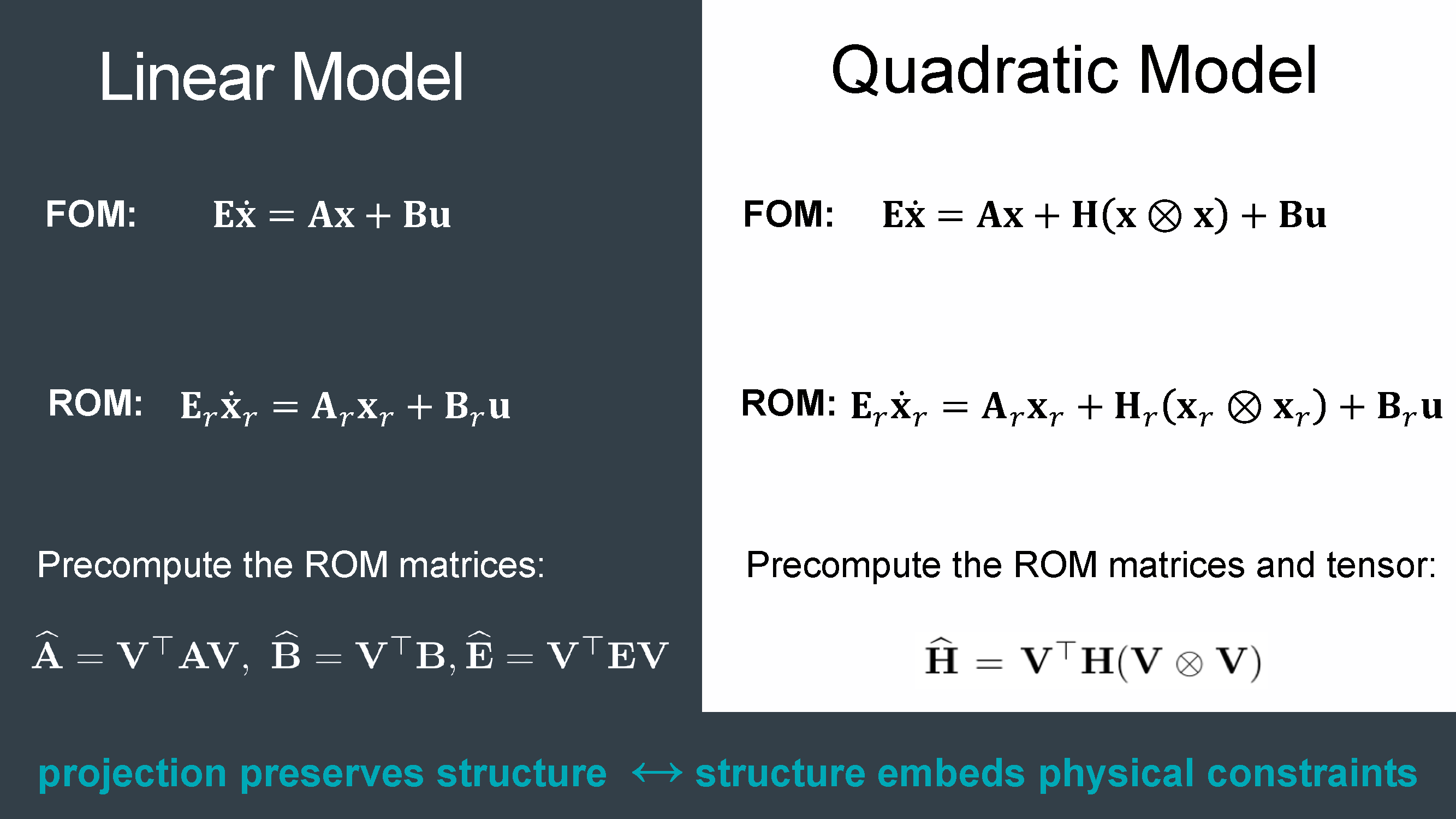
Lifting is a process that transforms a general nonlinear system into a structured polynomial system via variable transformations and the introduction of auxiliary variables. The lifted model is equivalent to the original model in that it uses a change of variables, but introduces no approximations. The lifted model has a polynomial form. Projection preserves this polynomial form in the reduced model. Operator Inference lets us learn a reduced model of the lifted form, by applying the lifting transformations to the snapshot data generated by the original code.
Lifting example
Suppose we want to transform a given scalar ODE with a quartic nonlinearity into a quadratic system. Via lifting, we introduce auxiliary variables. For each auxiliary variable, we derive a corresponding auxiliary equation by applying the chain rule. For the example below, we can choose to lift the model into (a) a system of four quadratic-bilinear (QB) ODEs, or (b) a system of two QB differential-algebraic equations (DAEs).

What kinds of models can be lifted?
Our work has shown that many of the partial differential equation (PDE) models that arise in science and engineering applications can be lifted to quadratic-bilinear (QB) form. See our papers for examples such as compressible flow, reacting flow, and rocket engine combustion.

What is the advantage of structure in the nonlinear model?
The primary advantage of the lifted model is that the polynomial form is preserved under projection, which means we can learn a structured polynomial reduced model via our data-driven Operator Inference method. This structure means that we do not need another layer of approximation (hyper-reduction) to gain computational efficiency. Exposing the system structure has additional benefits of opening new pathways for rigorous analysis, stability analysis, and input-independent model reduction.
Qian, E., Kramer, B., Peherstorfer, B., and Willcox, K., em>Physica D: Nonlinear Phenomena, to appear, 2020.
We present Lift & Learn, a physics-informed method for learning low-dimensional models for large-scale dynamical systems. The method exploits knowledge of a system's governing equations to identify a coordinate transformation in which the system dynamics have quadratic structure. This transformation is called a lifting map because it often adds auxiliary variables to the system state. The lifting map is applied to data obtained by evaluating a model for the original nonlinear system. This lifted data is projected onto its leading principal components, and low-dimensional linear and quadratic matrix operators are fit to the lifted reduced data using a least-squares operator inference procedure. Analysis of our method shows that the Lift & Learn models are able to capture the system physics in the lifted coordinates at least as accurately as traditional intrusive model reduction approaches. This preservation of system physics makes the Lift & Learn models robust to changes in inputs. Numerical experiments on the FitzHugh-Nagumo neuron activation model and the compressible Euler equations demonstrate the generalizability of our model.
Swischuk, R., Kramer, B., Huang, C. and Willcox, K., AIAA Journal, to appear, 2020.
This paper presents a physics-based data-driven method to learn predictive reduced-order models (ROMs) from high-fidelity simulations, and illustrates it in the challenging context of a single-injector combustion process. The method combines the perspectives of model reduction and machine learning. Model reduction brings in the physics of the problem, constraining the ROM predictions to lie on a subspace defined by the governing equations. This is achieved by defining the ROM in proper orthogonal decomposition (POD) coordinates, which embed the rich physics information contained in solution snapshots of a high-fidelity computational fluid dynamics (CFD) model. The machine learning perspective brings the flexibility to use transformed physical variables to define the POD basis. This is in contrast to traditional model reduction approaches that are constrained to use the physical variables of the high-fidelity code. Combining the two perspectives, the approach identifies a set of transformed physical variables that expose quadratic structure in the combustion governing equations and learns a quadratic ROM from transformed snapshot data. This learning does not require access to the high-fidelity model implementation. Numerical experiments show that the ROM accurately predicts temperature, pressure, velocity, species concentrations, and the limit-cycle amplitude, with speedups of more than five orders of magnitude over high-fidelity models. Our ROM simulation is shown to be predictive 200% past the training interval. ROM-predicted pressure traces accurately match the phase of the pressure signal and yield good approximations of the limit-cycle amplitude.
Kramer, B., and Willcox, K., arXiv:1907.12084. Submitted.
We present a balanced truncation model reduction approach for a class of nonlinear systems with time-varying and uncertain inputs. First, our approach brings the nonlinear system into quadratic-bilinear (QB) form via a process called lifting, which introduces transformations via auxiliary variables to achieve the specified model form. Second, we extend a recently developed QB balanced truncation method to be applicable to such lifted QB systems that share the common feature of having an indefinite system matrix. We illustrate this framework and the multi-stage lifting transformation on a tubular reactor model. In the numerical results we show that our proposed approach can obtain reduced-order models that are more accurate than proper orthogonal decomposition reduced-order models in situations where the latter are sensitive to the choice of training data.
Kramer, B. and Willcox, K., AIAA Journal, Vol. 57 No. 6, pp. 2297-2307, 2019.
This paper presents a structure-exploiting nonlinear model reduction method for systems with general nonlinearities. First, the nonlinear model is lifted to a model with more structure via variable transformations and the introduction of auxiliary variables. The lifted model is equivalent to the original model-it uses a change of variables, but introduces no approximations. When discretized, the lifted model yields a polynomial system of either ordinary differential equations or differential algebraic equations, depending on the problem and lifting transformation. Proper orthogonal decomposition (POD) is applied to the lifted models, yielding a reduced-order model for which all reduced-order operators can be pre-computed. Thus, a key benefit of the approach is that there is no need for additional approximations of nonlinear terms, in contrast with existing nonlinear model reduction methods requiring sparse sampling or hyper-reduction. Application of the lifting and POD model reduction to the FitzHugh-Nagumo benchmark problem and to a tubular reactor model with Arrhenius reaction terms shows that the approach is competitive in terms of reduced model accuracy with state-of-the-art model reduction via POD and discrete empirical interpolation, while having the added benefits of opening new pathways for rigorous analysis and input-independent model reduction via the introduction of the lifted problem structure.
Qian, E., Kramer, B., Marques, A. and Willcox, K., In Proceedings of AIAA Aviation Forum & Exhibition, Dallas, TX, June 2019.
This paper presents Transform & Learn, a physics-informed surrogate modeling approach that unites the perspectives of model reduction and machine learning. The proposed method uses insight from the physics of the problem — in the form of partial differential equation (PDE) models — to derive a state transformation in which the system admits a quadratic representation. Snapshot data from a high-fidelity model simulation are transformed to the new state representation and subsequently are projected onto a low-dimensional basis. The quadratic reduced model is then learned via a least-squares-based operator inference procedure. The state transformation thus plays two key roles in the proposed method: it allows the task of nonlinear model reduction to be reformulated as a structured model learning problem, and it parametrizes the machine learning problem in a way that recovers efficient, generalizable models. The proposed method is demonstrated on two PDE examples. First, we transform the Euler equations in conservative variables to the specific volume state representation, yielding low-dimensional Transform & Learn models that achieve a 0.05% relative state error when compared to a high-fidelity simulation in the conservative variables. Second, we consider a model of the Continuously Variable Resonance Combustor, a single element liquid-fueled rocket engine experiment. We show that the specific volume representation of this model also has quadratic structure and that the learned quadratic reduced models can accurately predict the growing oscillations of an unstable combustor.
Peherstorfer, B. and Willcox, K., Computer Methods in Applied Mechanics and Engineering, Vol. 306, pp. 196-215, 2016.
This work presents a nonintrusive projection-based model reduction approach for full models based on time-dependent partial differential equations. Projection-based model reduction constructs the operators of a reduced model by projecting the equations of the full model onto a reduced space. Traditionally, this projection is intrusive, which means that the full-model operators are required either explicitly in an assembled form or implicitly through a routine that returns the action of the operators on a given vector; however, in many situations the full model is given as a black box that computes trajectories of the full-model states and outputs for given initial conditions and inputs, but does not provide the full-model operators. Our non-intrusive operator inference approach infers approximations of the reduced operators from the initial conditions, inputs, trajectories of the states, and outputs of the full model, without requiring the full-model operators. Our operator inference is applicable to full models that are linear in the state or have a low-order polynomial nonlinear term. The inferred operators are the solution of a least-squares problem and converge, with sufficient state trajectory data, in the Frobenius norm to the reduced operators that would be obtained via an intrusive projection of the full-model operators. Our numerical results demonstrate operator inference on a linear climate model and on a tubular reactor model with a polynomial nonlinear term of third order.